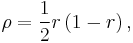Archimedean circle

In geometry, an Archimedean circle is any circle constructed from an arbelos that has the same radius as each of Archimedes' twin circles. The radius ρ of such a circle is given by

where r is the ratio AB/AC shown in the figure to the right. There are over fifty different known ways to construct Archimedean circles.^[1]

Origin

An Archimedean circle was first constructed by Archimedes in his Book of Lemmas. In his book, he constructed what is now known as Archimedes' twin circles.

Other Archimedean circles finders

Leon Bankoff

Leon Bankoff has constructed other Archimedean circles called Bankoff's triplet circle and Bankoff's quadruplet circle.

Thomas Schoch

In 1978 Thomas Schoch found a dozen more Archimedean circles (the Schoch circles) that have been published in 1998.^[2][3] He also constructed what is known as the Schoch line.^[4]

Peter Y. Woo

Peter Y. Woo considered the Schoch line, and with it, he was able to create a family of infinitely many Archimedean circles known as the Woo circles.^[5]

Frank Power

In the summer of 1998, Frank Power introduced four more Archimedes circles known as Archimedes' quadruplets.^[6]

References